꽃, 솔방울, 조개, 과일, 허리케인, 심지어 나선은하까지 모두 피보나치 수열을 나타냅니다.
피보나치 수열이란?
1, 1, 2, 3, 5, 8, 13, 21… 피보나치 수열. 시퀀스의 모든 숫자는 이전 두 숫자를 더하여 생성됩니다. 따라서 다음 피보나치 수는 13 + 21 = 34입니다. 이들은 각 숫자가 시퀀스의 이전 숫자에 있는 방정식에 의해 생성되는 재귀 시퀀스의 가장 간단한 예입니다.
이 수열 안에는 수학에서 또 다른 중요한 숫자인 황금 비율이 숨겨져 있습니다. 그리스 문자 파이로 표시되며 패턴이 없는 무한 소수점 확장을 갖는 파이와 같은 숫자입니다. phi = 1.61803으로 시작합니다... A/B 비율이 (A + B)/A와 동일한 A x B 치수의 직사각형 비율로 정의됩니다.
이것은 많은 예술가들이 캔버스의 완벽한 비율로 간주합니다. 피보나치 수열의 숫자를 수열의 이전 수(예: 5/3)로 나누면 이 분수는 점점 더 큰 피보나치 수를 취함에 따라 황금비에 점점 더 가까워집니다. 이전의 모든 숫자를 계산할 필요가 없도록 하는 황금 비율과 관련된 피보나치 수에 대한 공식이 있습니다.
이 숫자에 대해서는 아직 수수께끼가 있습니다. 예를 들어, 소수이기도 한 피보나치 수는 무한히 많이 있을까요? 2, 3, 5, 13처럼... 우리는 51개의 피보나치 소수만 알고 있지만 무한대가 있을 수 있을까요?
피보나치 수는 왜 그렇게 중요한가?
피보나치 수는 자연이 가장 좋아하는 숫자입니다. 당신은 자연 세계에서 그들을 찾을 수 있습니다. 꽃의 꽃잎 수를 세어보면 종종 피보나치 수입니다. (그렇지 않다면, 그것은 꽃잎이 당신의 꽃에서 떨어졌음을 의미합니다. 이것이 수학자들이 예외를 피하는 방법입니다).
과일을 자르면 종종 피보나치 수의 팔이 있는 별 모양을 찾을 수 있습니다. 바나나에는 꼭지점이 세 개, 사과에 꼭지점이 다섯 개, 감에 꼭지점이 여덟 개 있습니다. 파인애플의 세포를 세어보면 여러 개의 피보나치 수를 찾을 수 있습니다. 해바라기의 씨앗은 또한 효율적으로 포장하기 위해 피보나치 수를 이용합니다.
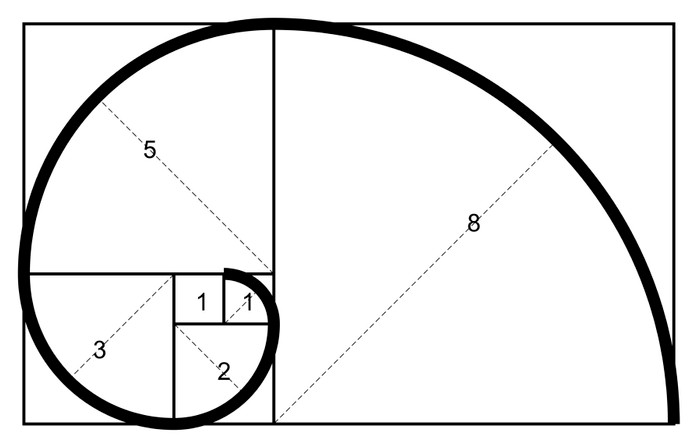
피보나치는 이러한 숫자가 자연 세계에서 사물이 어떻게 성장하는지의 핵심이라고 설명했습니다. 자연은 지금까지 성장한 것을 사용하여 다음 조치를 취합니다. 치수가 피보나치 수에 해당하는 정사각형을 취하면 확장 직사각형으로 배열할 수 있습니다. 이는 그것이 어떻게 사물을 성장시키는 데 도움이 되며 왜 나선형을 발생시키는지를 설명합니다.
피보나치는 또한 이 숫자가 토끼의 인구 증가를 추적하는 방법을 설명했습니다. 한 쌍의 토끼가 새 한 쌍의 토끼를 낳기 전에 성숙하는 데 한 달이 걸린다면, 한 달에 몇 쌍의 토끼가 있습니까? 정답은 피보나치 수열에 있습니다.

피보나치는 누구였습니까?
숫자는 레오나르도 보나치라고도 알려진 피사의 13세기 이탈리아 수학자 이름을 따서 명명되었습니다. 그는 1853년 역사가 Guillaume Libri가 그를 피보나치라고 부르기 시작하면서 피보나치라는 이름으로 널리 알려지게 되었습니다.
피보나치는 1202년에 출판된 Liber Abaci 라는 매우 영향력 있는 책에서 이 숫자에 대해 썼습니다 .
그의 책은 계산을 수행하는 새로운 방법에 대한 도움을 의미했으며 새로운 힌두 아라비아 숫자의 힘을 설명합니다. 그는 북아프리카를 여행하면서 이 새로운 숫자에 대해 배웠습니다. 유럽에서는 여전히 로마 숫자와 주판을 사용하여 계산했습니다. 그러나 주판을 사용하려면 기술과 전문 지식이 필요했습니다. 그것은 계산이 일반 시민이 사용할 수 있는 것이 아니라는 것을 의미했습니다.
Fibonacci는 서투른 로마 숫자를 사용하는 대신 인도인들이 0이라는 혁신적인 신개념과 함께 1에서 9까지의 숫자를 활용하여 자릿수 체계를 사용하여 효율적으로 숫자를 표현하는 방법을 설명했습니다. 피보나치의 책은 일반 시민에게 계산에 대한 액세스 권한과 이러한 계산을 기록할 수 있는 기능을 제공했습니다. 이것이 설립 초기에 동양에서 들어오는 숫자를 금지하려고 시도한 이유입니다.
그의 책은 중세 기간 동안 유럽에서 수학을 시작하는 데 책임이 있습니다. 그가 지금 그의 이름을 딴 일련의 숫자를 소개한 것은 Liber Abaci 라는 책 입니다.

이 숫자를 처음 발견한 사람은 피보나치입니까?
아니! 이 숫자는 실제로 피보나치보다 수세기 전에 발견한 인도 시인과 음악가의 이름을 따서 명명되어야 합니다. 자연보다는 음악과 시의 리듬을 이해하는 것이 발견의 비결이었습니다.
장박과 짧은 박을 합치면 드럼에서 얼마나 많은 다른 리듬을 만들 수 있습니까? 예를 들어, 긴 비트가 짧은 비트의 두 배인 경우 길이 4로 만들 수 있는 리듬의 수는 다음과 같습니다. SHORT-SHORT-SHORT-SHORT, LONG-SHORT-SHORT, SHORT-LONG-SHORT, SHORT-SHORT- 롱, 롱-롱. 총 5개의 다른 리듬. 피보나치 수!
길이가 5인 리듬을 만들고 싶다면 길이가 3인 세 개의 리듬에 LONG 비트를 추가하거나 길이가 4인 다섯 개의 리듬에 SHORT 비트를 추가할 수 있습니다. 길이가 5인 8개의 리듬이 있습니다. 리듬의 수는 피보나치 규칙에 따라 늘어납니다.
많은 현대 음악가들이 작업에 피보나치 수를 사용하는 것을 즐겼습니다. 예를 들어, Debussy는 그의 작품 La Mer 에서 Bartok이 그의 Music For Strings, Percussion And Celesta 에서 사용하는 것처럼 그것들을 사용합니다 . 피보나치 수열에 해당하는 음절이 각 행에 있는 Fib라고 하는 새로운 형태의 시도도 있습니다.
'과학기술' 카테고리의 다른 글
| [우주과학] 대체 타임라인과 다중우주에 대한 물리학적 설명! (0) | 2022.08.23 |
|---|---|
| [자연과학] 하늘을 나는 동물 7가지 (ft.조류제외) (0) | 2022.08.21 |
| [인체과학] 죽은 후에 몸은 어떤 현상이 일어날까요?! 7단계 변화 (0) | 2022.08.18 |
| [우주과학] 빅뱅 이전에는 무엇이 있었을까요? (0) | 2022.08.16 |
| [물리과학] 과학자들은 시간을 거꾸로 달리는 '반우주'가 있다고 말한다 (0) | 2022.08.12 |




댓글